Haugh Transform

This is a learning note related to the Haugh Transform. It contains its basic idea and implementation (compare with function from libraty).

Haugh Transform

Basic ideas

The basic idea is transform each node from the image space to parameter space.

For example, in the image space x-y, a line can be expressed:

where k and b are parameters, indicating the slope and intercept of the line.

For all lines which passed on point $A(x_1, y_1)$ meet the function $y_1 = m *x_1 + b$. In other words, point $A(x_1, y_1)$ indentify a group of straight lines. If we rewrute the equation as $b = -mx_1 + y_1$. Then the equation corresponds to a straight line in the parameter space k-b.

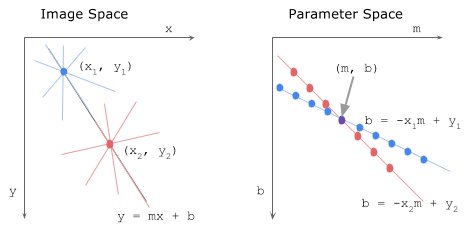
Therefore, it can be concluded that the points in the image space correspond to the straight lines in the parameter space one by one.

Also, from Fig.1, there are two points A and B in the image space, correspondingly, in parameter space there are two straight lines. The corresponding straight lines intersect at a point in the parameter space k-b, which means that the straight line determined by A B corresponds to a unique point in the parameter space, and the coordinate value of this point $(m, b)$ is also the parameter of the straight line AB.

In order to explain the basic principles of Hough transformation, we chose Cartesian rectangular coordinate system as our parameter space. However, in practical applications, the parameter space cannot choose a rectangular coordinate system, because the special straight line $x = c$ (vertical x axis, the slope of the straight line is infinite) in the image space cannot be expressed in the parameter space based on the rectangular coordinate system.

So can we use other ways to represent it? Of course, generally we use polar coordinates as the parameter space.

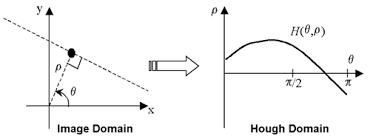
Where

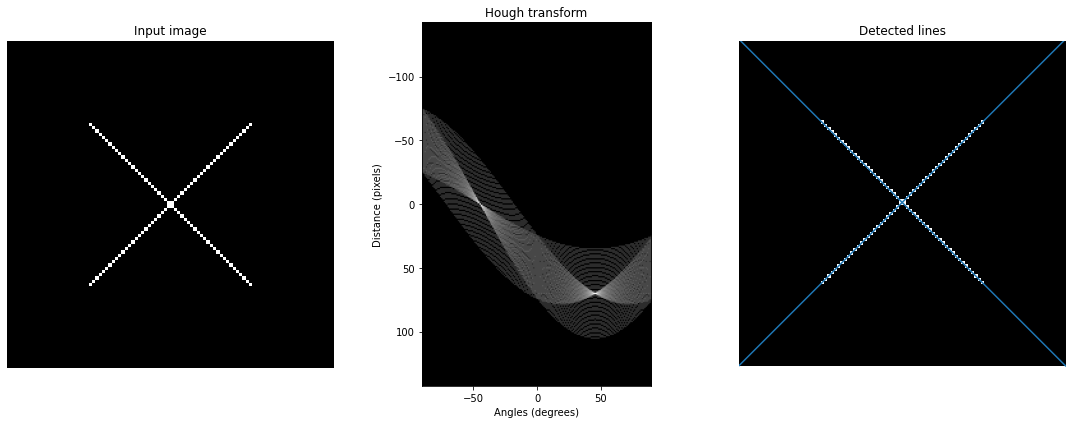
Numerous points in image space corresponds to numerous lines in parameter space (Haugh Domain) which all interacte at one point

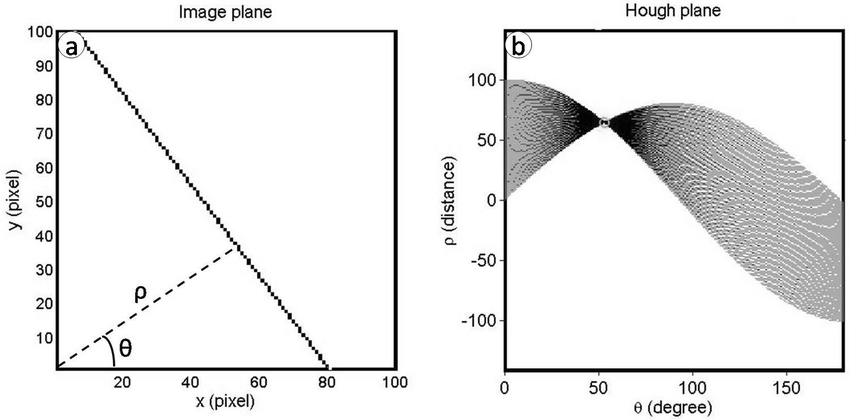
The interation point is the $(\theta, \rho)$ pair we want. In haugh, the negative $\rho$ doesn’t mean the distance is negative but different direction.

Implementation

There are four basic steps for Haugh Transform:

• Edge detection
• Decide number of theta and d bins (ntheta,nd). Create accumulator image H[ntheta,nd]
• Voting: For each edge and theta calculate d and and H[theta, d] += 1
• Optional: Find peaks in accumulator image

# implement hough transform function
def hough(img, peaks_num):
  # first step: Edge detection by using canny
  # here I am using a binary image, so I don't need to detect the edge
  edge = img

  # second step: decide the number of theta and d bins (ntheta, nb), 
  # create the Haugh transform accumulator H[ntheta, nb]
  thetas = np.deg2rad(np.linspace(-90,89,180))
  ntheta = len(thetas)
  nrho = int(np.ceil(np.sqrt(img.shape[0]**2 + img.shape[1]**2)))
  rhos = np.linspace(-nrho, nrho-1, 2*nrho)
  H = np.zeros((2*nrho, ntheta))
  print(H.shape)

  # third step: Voting
  # For each edge and theta calculate d and H[theta, d] += 1
  y_index, x_index = np.nonzero(edge)
  for i in range(len(x_index)):
    x = x_index[i]
    y = y_index[i]
    for theta in range(ntheta):
      if theta >= 90:
        d = int(x*np.cos(thetas)[theta] + y*np.sin(thetas)[theta]) + nrho
      else:
        d = int(x*np.cos(thetas)[theta] + y*np.sin(thetas)[theta]) - nrho
      H[d, theta] += 1
  
  # Forth step: Find peaks in Haugh space image H
  H_ = np.ravel(H)
  H_ = np.argsort(H_)[::-1]
  peaks_index = H_[:peaks_num]
  peaks_angle = (peaks_index % ntheta)-90
  peaks_d = (peaks_index / ntheta).astype(int)-nrho
  
  return peaks_angle, peaks_d, thetas, rhos, H

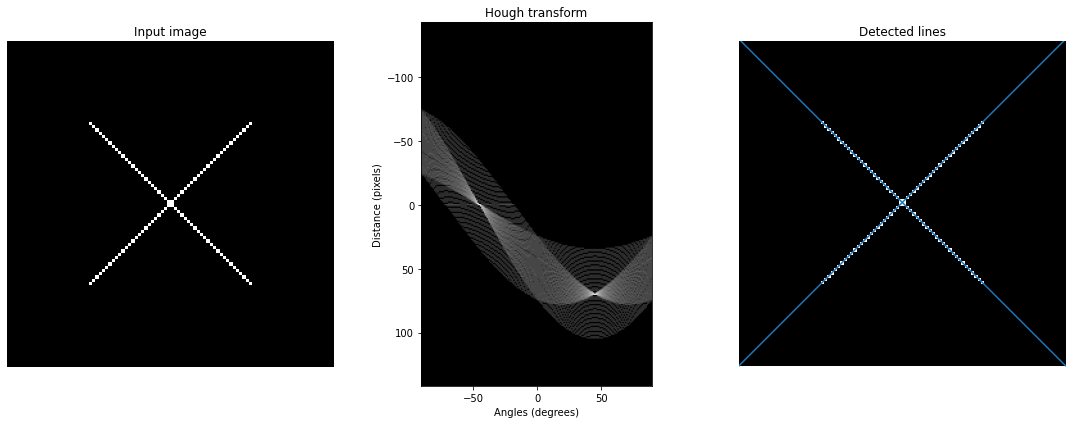
All code can be found here

Reference1 Reference2