Dice Coefficient & Dice Loss

This is a learning note related to the Dice Coefficient and corresponding Dice Loss. It contains their basic idea and implementations.

Dice Coefficient

Basic ideas

Dice coefficient is evaluation criteria of sementic segmentation. By computing the overlap ratio between ground truth and predicted segmentation, it reflects the similarity between them. Its value is in range [0, 1]. The bigger the values is, the more area overlapped, the beeter the segmentation result.

The function is:

where $|X\cap Y|$ is the intersaction between $X$ and $Y$, $|X|$ and $|Y|$ represent the number of elements in $X$ and $Y$, the reason why coefficient of the numerator is 2 is that the denominator repeatedly calculate the common element between X and Y.

More intuitively, the function can be illustrated as following:

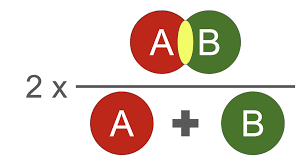
For the semantic segmentation problem, $X$ is the ground truth while Y is the predicted segmentation.

Implementation

def dice_coeff(input, target):
    smooth = 1.
    iflat = input.view(-1)
    tflat = target.view(-1)
    intersection = (iflat * tflat).sum()
    return ((2. * intersection + smooth) /
            (iflat.sum() + tflat.sum() + smooth))

Dice Loss

Basic ideas

Dice Loss is the difference between 1 and dice coefficient.

Implementation

def dice_coeff(input, target):
    smooth = 1.
    iflat = input.view(-1)
    tflat = target.view(-1)
    intersection = (iflat * tflat).sum()
    return ((2. * intersection + smooth) /
            (iflat.sum() + tflat.sum() + smooth))

def dice_loss(input, target):
    return 1 - dice_coeff(input, target)